If the Powerball Jackpot hits $1.7 Billion, it will actually be +EV to play

[festeringZit]

[h=2]The One Time It’s Mathematically Advantageous to Play Powerball[/h]
<time class="modified-date" datetime="2016-01-10 20:31:32"></time>


<section class="article-body" itemprop="articleBody"> [h=2]If the jackpot gets big enough, it's actually worth your while to play the lottery.[/h] <figure class="primary-video-wrapper video-brightcove" itemprop="video"></figure> <aside class="right-rail__container right-rail__container--ad"> <svg id="sh-poll-icon-svg" xmlns="http://www.w3.org/2000/svg" x="0px" y="0px" width="13px" height="13px" viewBox="0 0 13 13" xml:space="preserve"><g id="sh-poll-bars">
</path>
</path>
</path></g></svg>








</aside>
</section><aside class="right-rail__container">


</aside> Wednesday’s Powerball jackpot is on its way to an estimated $1.3 billion, after nobody matched all six numbers in Saturday night’s drawing. The prize would be the biggest of all time, dwarfing the MegaMillions $656 million high-water mark of 2012. This is a big deal.
Unless you’re really, really smart and lucky—see Joan Ginther, among others—playing the lottery is a bad idea, financially speaking. Of course there’s the fun, thrilling aspect of playing, which is not to be discounted, even by a belt-and-suspenders-type publication like MONEY.
But there’s actually a case to be made that in some rare instances, it’s mathematically advantageous to roll the dice on some Powerball, or other lottery tickets. When a jackpot grows, it brings up the value of a ticket, which in Powerball’s case costs $2. That’s called the expected value, and it’s found by multiplying the payout by the probability of winning.
Here’s a simple example: In a basic lottery with just one prize, $1 tickets, and 100 people playing, any jackpot over $100 will mean that a ticket will be worth more than the $1 it costs. If you bought all the tickets for $100, you would win the jackpot and take home more than what you paid. So theoretically, at a certain size, a lottery ticket can actually be worth more than what you pay for it.


Still, if a jackpot is huge and a $2 ticket somehow gets to be theoretically worth $2.02, you’d have to buy a very large amount of tickets to see returns, similar to how the very slight odds a casino make it money over time. For fun, let’s see how high a jackpot would have to be to make mathematical sense to play.
First of all, there are three major things winners have to contend with—taxes, the lump sum discount, and potentially splitting the pot with other people.
[h=3]The simple version[/h] There are other prizes besides the jackpot, but for simplicity’s sake, just to get a ballpark figure, we can discount them because they’re pretty insignificant. To find out how big a jackpot you’d need to get the value of a ticket to be equal or greater to than what you paid, you just divide the cost by the probability, which you can calculate by dividing one (1) by the odds. (That’s 1/292,201,338 in this case.) That equals around $584 million. And that’s what the take-home sum needs to be to make it worthwhile to play.
If we add what would be taken out in federal income taxes (39.4%)—this exercise assumes you live in New Hampshire and don’t pay state income taxe—by dividing by 0.606 (1-0.394), we get $974 million as the necessary pre-tax sum for the jackpot.
But then we have to contend with the possibility of multiple winners with and a split pot, which gets more and more likely as more tickets get sold. DurangoBill.com has a great chart that works those probabilities out, and if 200 million tickets are sold, a jackpot’s value goes down about 16% when you account for the possibility of multiple winners. So $974 million divided by 0.84 (1-0.26) comes to… a lump sum pre-tax cash payout of $1.2 billion. This is the ballpark we’re working with.
[h=3]The complicated version[/h] But the “break even” jackpot is actually a little lower! There are, after all, plenty of other prizes at stake. To adjust for those, it’s helpful to find out how much they’re worth, again by finding their expected value.
Adding up the expected values for all those prizes absenting the jackpot comes to $0.24 (for each prize: Prize x probability+prize x probability + etc.). So the jackpot’s contribution to the total expected value of a Powerball ticket can drop $.024. Since a ticket costs $2, we only need the jackpot’s portion of the ticket’s expected value to be $1.76 in order to have a a ticket that’s worth what it costs—and a break-even system.
So since we know we need the expected value of the jackpot’s portion a Powerball ticket’s worth ($1.76), we can find out how big the jackpot needs to be, just like we did in the simple version. By dividing the $1.76 by the probability of hitting it big, adjusting for taxes, adjusting for jackpot splitting, you get… $1.02 billion. But this is just the cash payout, which is usually three-fifths of the jackpot.


If the billboards and newscasters ever announce a $1.7 billion Powerball, the math’s likely to be in your favor.
Now, that’s figure is with a very conservative 200 million tickets sold. If the jackpot actually gets this big, far more tickets could be sold, making the likelihood of a split higher and driving the value of a ticket down—so you’d have to again wait for an increase in jackpot size raise the expected value of a ticket. But then, of course, more people would play, and the single-winner probability would drop again. It’s a vicious cycle.
You can, however, do a few little things to increase your chances, most notably by trying to choose numbers that are off the beaten path. Think about numbers people are more likely to choose (dates, so numbers under 31, for example). Don’t choose them. Think about ways people might pick numbers, and avoid them. For instance, people tend to think winning lotto numbers will all be across the spectrum. But 43-44-41-42-40-(25) is just as likely as any other. Humans are awful at picking randomly so use that to your advantage.
Is this all realistic? Well, yeah. It’s not unheard of for a lottery to be in your favor, although it’s not likely to happen very often: $1.7 billion is pretty high. But it could happen. And if so, remember to enjoy that $2 dream when you play.

_____________________

 

[festeringZit]

[SIZE=+2][SIZE=+1]Powerball Odds

How to Calculate the Odds and Probabilities for the
Powerball Lottery[/SIZE]

[/SIZE] Powerball odds and probabilities for the Powerball Jackpot – and how to calculate these Powerball odds. Additional calculations show tie probabilities and expected return on your “investment”.

[SIZE=+2]Updated for the 69/26 Game[/SIZE]
​

Concise Table of Powerball Odds (Mathematical derivation below)
​

[SIZE=-1]Ticket Matches Payout Odds Probability
--------------------------------------------------------------------
5 White + PB Jackpot 1 in 292,201,338.00 0.000000003422
5 White No PB 1,000,000 1 in 11,688,053.52 0.00000008556
4 White + PB 50,000 1 in 913,129.18 0.000001095
4 White No PB 100 1 in 36,525.17 0.00002738
3 White + PB 100 1 in 14,494.11 0.00006899
3 White No PB 7 1 in 579.76 0.001725
2 White + PB 7 1 in 701.33 0.001426
1 White + PB 4 1 in 91.98 0.01087
0 White + PB 4 1 in 38.32 0.02609

Win something Variable 1 in 24.87 0.0402[/SIZE]

[SIZE=+1]Game Rules[/SIZE]
The numbers picked for the prizes consist of 5 white balls picked at random from a drum that holds 69 balls numbered from 1 to 69. The Powerball number is a single ball that is picked from a second drum that has 26 numbers ranging from 1 to 26. If the results of these random number selections match one of the winning combinations on your lottery ticket, then you win something.

You can also buy a “Power Play” option. The multipliers in the 69/26 Power Play game increase the payout amounts for the non-jackpot prizes as shown in the “Power Play Option” section. (Scroll down the page.)

In the game version that began as of Jan. 15, 2012, it costs $2 to buy a ticket instead of the previous $1. The Power Play option costs another $1; and as noted above, the payout amounts have been changed.

[SIZE=+1]Game Rules for the new Powerball game that went into effect for the Oct. 7, 2015 game.[/SIZE]
​

As “game players” (“suckers”) woke up to the fact that they were throwing money away trying to win the old 59/35 game, Powerball ticket sales slumped. Thus Powerball officials changed the game rules again to try to recruit more people to throw away their money.

The new game is designed to “engineer” bigger jackpots. The mechanism involved was to make it even more difficult to win. Thus funds that previously had been paid out to “millionaire” winners will now be retained until a possible “billionaire” figure is reached.

In the old version of the game, the chance of winning the jackpot was one chance in COMBIN(59,5) x COMBIN(35,1) = 175,223,510. The new version of the game has 69 balls in one bin and 26 in the other. Thus the chance of winning the new game is 1 chance in COMBIN(69,5) x COMBIN(26,1) = 292,201,338. In practical terms, it would appear likely that few people will buy tickets for most jackpots, but buying frenzies will develop for large jackpots. (With the resulting prize split several ways.)

Imagine lining up baseballs (A standard baseball is about 2.9 inches in diameter.) in a row for the 2,998.68 highway miles from Boston to Los Angeles (Mapquest). It would take about 65,515,988 baseballs. Then randomly designate one of these baseballs as a lucky “winner” baseball.

Imagine driving for days past this row of millions and millions of baseballs. Then stop and pick up a random baseball. The chance of a random ticket winning the new Powerball is less than one fourth the chance of picking the winning baseball.

The phrase “There's a sucker born every minute” comes to mind. (Falsely attributed to P. T. Barnum https://en.wikipedia.org/wiki/There's_a_sucker_born_every_minute )



In any combinatorics problem where all possible outcomes are equally likely, the probability of a successful outcome is determined by finding the number of successful combinations, and then dividing by the total number of all combinations. There are nine possible configurations that will win something in the Powerball Lottery. For each of these, the probability of winning equals the number of winning combinations for that particular configuration divided by the total number of ways the Powerball numbers can be picked.



[SIZE=+1]Powerball Total Combinations[/SIZE]
Since the total number of combinations for Powerball numbers is used in all the calculations, we will calculate it first. The number of ways 5 numbers can be randomly selected from a field of 69 is: COMBIN(69,5) = 11,238,513. (See the math notation page or Help in Microsoft's Excel for more information on “COMBIN”).

For each of these 11,238,513 combinations there are COMBIN(26,1) = 26 different ways to pick the Powerball number. The total number of ways to pick the 6 numbers is the product of these. Thus, the total number of equally likely Powerball combinations is 11,238,513 x 26 = 292,201,338. We will use this number for each of the following calculations.


[SIZE=+1]Jackpot probability/odds (Payout varies)[/SIZE]
The number of ways the 5 numbers on your lottery ticket can match the 5 white balls is COMBIN(5,5) = 1. The number of ways your Powerball number can match the single Powerball number is: COMBIN(1,1) = 1. The product of these is the number of ways you can win the Jackpot: COMBIN(5,5) x COMBIN(1,1) = 1. The probability of success is thus: 1/292,201,338 = 0.000000003422297813+. If you express this as “One chance in ???”, you just divide “1” by the 0.000000003422297813+, which yields “One chance in 292,201,338”.


[SIZE=+1] Match all 5 white balls but not the Powerball (Payout = $1,000,000)[/SIZE]
The number of ways the 5 numbers on your lottery ticket can match the 5 white balls is COMBIN(5,5) = 1. The number of ways your Powerball number can match any of the 25 losing Powerball numbers is: COMBIN(25,1) = 25. (Pick any of the 25 losers.) Thus there are COMBIN(5,5) x COMBIN(25,1) = 25 possible combinations. The probability for winning $1,000,000 is thus 25/292,201,338 ~= 0.00000008556 or “One chance in 11,688,053.52”.


[SIZE=+1]Match 4 out of 5 white balls and match the Powerball (Payout = $50,000)[/SIZE]
The number of ways 4 of the 5 winning numbers on your lottery ticket can match the 5 white balls is COMBIN(5,4) = 5. The number of ways the losing white number on your ticket can match any of the 64 losing white numbers is COMBIN(64,1) = 64. The number of ways your Powerball number can match the single Powerball number is: COMBIN(1,1) = 1. The product of these is the number of ways you can win this configuration: COMBIN(5,4) x COMBIN(64,1) x COMBIN(1,1) = 320. The probability of success is thus: 320/292,201,338 ~= 0.000001095 or “One chance in 913,129.18”.


[SIZE=+1]Match 4 out of 5 white balls but not match the Powerball (Payout = $100)[/SIZE]
The number of ways 4 of the 5 winning numbers on your lottery ticket can match the 5 white balls is COMBIN(5,4) = 5. The number of ways the losing white number on your ticket can match any of the 64 losing numbers is COMBIN(64,1) = 64. The number of ways your Powerball number can miss matching the single Powerball number is: COMBIN(25,1) = 25. The product of these is the number of ways you can win this configuration: COMBIN(5,4) x COMBIN(64,1) x COMBIN(25,1) = 8,000. The probability of success is thus: 8,000/292,201,338 ~= 0.00002738 or “One chance in 36,525.17”.


[SIZE=+1]Match 3 out of 5 white balls and match the Powerball (Payout = $100)[/SIZE]
The number of ways 3 of the 5 winning numbers on your lottery ticket can match the 5 white balls is COMBIN(5,3) = 10. The number of ways the 2 losing white numbers on your ticket can match any of the 64 losing white numbers is COMBIN(64,2) = 2,016. The number of ways your Powerball number can match the single Powerball number is: COMBIN(1,1) = 1. The product of these is the number of ways you can win this configuration: COMBIN(5,3) x COMBIN(64,2) x COMBIN(1,1) = 20,160. The probability of success is thus: 20,160/292,201,338 ~= 0.00006899 or “One chance in 14,494.11”.


[SIZE=+1]Match 3 out of 5 white balls but not match the Powerball (Payout = $7)[/SIZE]
The number of ways 3 of the 5 winning numbers on your lottery ticket can match the 5 white balls is COMBIN(5,3) = 10. The number of ways the 2 losing white numbers on your ticket can match any of the 64 losing numbers is COMBIN(64,2) = 2,016. The number of ways your Powerball number can miss matching the single Powerball number is: COMBIN(25,1) = 25. The product of these is the number of ways you can win this configuration: COMBIN(5,3) x COMBIN(64,2) x COMBIN(25,1) = 504,000. The probability of success is thus: 504,000/292,201,338 ~= 0.001725 or “One chance in 579.76”.


[SIZE=+1]Match 2 out of 5 white balls and match the Powerball (Payout = $7)[/SIZE]
The number of ways 2 of the 5 winning numbers on your lottery ticket can match the 5 white balls is COMBIN(5,2) = 10. The number of ways the 3 losing white numbers on your ticket can match any of the 64 losing white numbers is COMBIN(64,3) = 41,664. The number of ways your Powerball number can match the single Powerball number is: COMBIN(1,1) = 1. The product of these is the number of ways you can win this configuration: COMBIN(5,2) x COMBIN(64,3) x COMBIN(1,1) = 416,640. The probability of success is thus: 416,640/292,201,338 ~= 0.001426 or “One chance in 701.33”.


[SIZE=+1]Match 1 out of 5 white balls and match the Powerball (Payout = $4)[/SIZE]
The number of ways 1 of the 5 winning numbers on your lottery ticket can match the 5 white balls is COMBIN(5,1) = 5. The number of ways the 4 losing white numbers on your ticket can match any of the 64 losing white numbers is COMBIN(64,4) = 635,376. The number of ways your Powerball number can match the single Powerball number is: COMBIN(1,1) = 1. The product of these is the number of ways you can win this configuration: COMBIN(5,1) x COMBIN(64,4) x COMBIN(1,1) = 3,176,880. The probability of success is thus: 3,176,880/292,201,338 ~= 0.01087 or “One chance in 91.98”.


[SIZE=+1]Match 0 out of 5 white balls and match the Powerball (Payout = $4)[/SIZE]
The number of ways 0 of the 5 winning numbers on your lottery ticket can match the 5 white balls is COMBIN(5,0) = 1. The number of ways the 5 losing white numbers on your ticket can match any of the 64 losing white numbers is COMBIN(64,5) = 7,624,512. The number of ways your Powerball number can match the single Powerball number is: COMBIN(1,1) = 1. The product of these is the number of ways you can win this configuration: COMBIN(5,0) x COMBIN(64,5) x COMBIN(1,1) = 7,624,512. The probability of success is thus: 7,624,512/292,201,338 ~= 0.02609 or “One chance in 38.32”.


[SIZE=+1]Probability of winning something[/SIZE]
If we add all the ways you can win something we get:
1 + 25 + 320 + 8,000 + 20,160 + 504,000 + 416,640 + 3,176,880 + 7,624,512 = 11,750,538. If we divide this number by 292,201,338, we get .04021+ as a probability of winning something. 1 divided by 0.04021- yields “One chance in 24.87” of winning something.


[SIZE=+1]Corollary[/SIZE]
You can get a close estimate for the number of tickets that were in play for any given game by multiplying the announced number of “winners” by the above 24.87. Thus, if the lottery officials proclaim that a given lottery drawing had 3 million “winners”, then there were about 3,000,000 x 24.87 ~= 74,601,181 tickets purchased that did not win the Jackpot. Alternately, there were about 74,601,181 - 3,000,000 ~= 71,601,181 tickets that did not win anything.

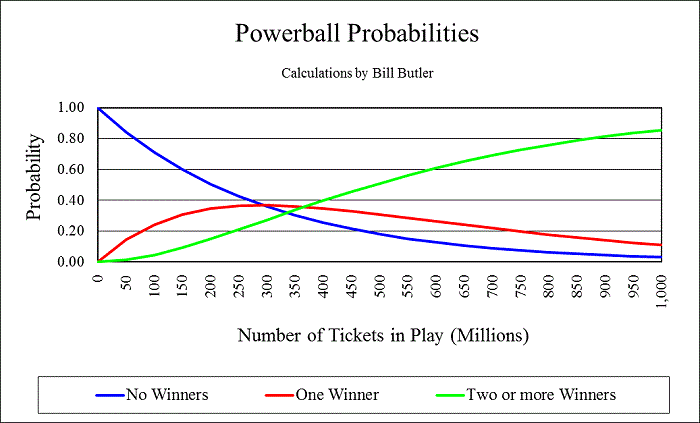
[SIZE=+1]Probability of multiple winning tickets (multiple winners) given “N” tickets in play[/SIZE]
​

(Note: All calculations assume that the numbers on any given ticket are picked randomly. In practice, many people pick numbers based on family birthdays, etc., and thus many tickets will have a preponderance of low numbers. As a consequence, the probabilities of a single Jackpot winner will be somewhat lower and the probabilities of no winner or multiple winners will tend to be slightly higher than the numbers shown below. Also if the numbers picked in the drawing are clustered at the high end of the 1-69 range, there will tend to be relatively less “partial match” winners. The reverse will hold true if the drawing numbers cluster in the low end of the number range.)

​

The above chart shows the probabilities of “No Winners”, “One Winner”, and “Two or more Winners” for various numbers of tickets in play.

Each entry in the following table shows the probability of "K" tickets holding the same winning Jackpot combination given that "N" tickets are in play for a given Powerball game. It is assumed that the number selections on each ticket are picked randomly. For example, if 100,000,000 tickets are in play for a Powerball game, then there is a 0.0416 probability that exactly two of these tickets will have the same winning combination.

(Note: You can get a rough estimate of the number of tickets in play as follows. If the preceding Powerball game had no Jackpot winner, multiply the dollar increase in the Jackpot from the preceding game to the current game by 3/2. (Use the cash payout amount). For example, if the preceding game had a cash payout amount of $100,000,000 and the current game has a cash payout amount of $120,000,000, then there are about (3/2) x (120,000,000 – 100,000,000) = 30,000,000 tickets in play for the current game. (Each ticket sold for $2.) A history of these past jackpot amounts (subtract about 50 % from the stated jackpot amount to get the cash payout) can be seen at:
http://www.lottostrategies.com/script/jackpot_history/draw_date/101)


[SIZE=-1]“N” Number “K”
of tickets Number of tickets holding the Jackpot combination
in play 0 1 2 3 4 5 6 7 8
--------------------------------------------------------------------[/SIZE][SIZE=-1]----------------[/SIZE][SIZE=-1]-[/SIZE]
[SIZE=-1]20,000,000 0.9338 0.0639 0.0022 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
40,000,000 0.8721 0.1194 0.0082 0.0004 0.0000 0.0000 0.0000 0.0000 0.0000
60,000,000 0.8144 0.1672 0.0172 0.0012 0.0001 0.0000 0.0000 0.0000 0.0000
80,000,000 0.7605 0.2082 0.0285 0.0026 0.0002 0.0000 0.0000 0.0000 0.0000
100,000,000 0.7102 0.2430 0.0416 0.0047 0.0004 0.0000 0.0000 0.0000 0.0000
120,000,000 0.6632 0.2724 0.0559 0.0077 0.0008 0.0001 0.0000 0.0000 0.0000
140,000,000 0.6193 0.2967 0.0711 0.0114 0.0014 0.0001 0.0000 0.0000 0.0000
160,000,000 0.5784 0.3167 0.0867 0.0158 0.0022 0.0002 0.0000 0.0000 0.0000
180,000,000 0.5401 0.3327 0.1025 0.0210 0.0032 0.0004 0.0000 0.0000 0.0000
200,000,000 0.5044 0.3452 0.1181 0.0270 0.0046 0.0006 0.0001 0.0000 0.0000
220,000,000 0.4710 0.3546 0.1335 0.0335 0.0063 0.0009 0.0001 0.0000 0.0000
240,000,000 0.4398 0.3613 0.1484 0.0406 0.0083 0.0014 0.0002 0.0000 0.0000
260,000,000 0.4107 0.3655 0.1626 0.0482 0.0107 0.0019 0.0003 0.0000 0.0000
280,000,000 0.3836 0.3675 0.1761 0.0562 0.0135 0.0026 0.0004 0.0001 0.0000
300,000,000 0.3582 0.3678 0.1888 0.0646 0.0166 0.0034 0.0006 0.0001 0.0000
320,000,000 0.3345 0.3663 0.2006 0.0732 0.0200 0.0044 0.0008 0.0001 0.0000
340,000,000 0.3124 0.3635 0.2115 0.0820 0.0239 0.0056 0.0011 0.0002 0.0000
360,000,000 0.2917 0.3594 0.2214 0.0909 0.0280 0.0069 0.0014 0.0002 0.0000
380,000,000 0.2724 0.3543 0.2303 0.0999 0.0325 0.0084 0.0018 0.0003 0.0000
400,000,000 0.2544 0.3482 0.2383 0.1088 0.0372 0.0102 0.0023 0.0005 0.0001
420,000,000 0.2376 0.3415 0.2454 0.1176 0.0422 0.0121 0.0029 0.0006 0.0001
440,000,000 0.2218 0.3340 0.2515 0.1262 0.0475 0.0143 0.0036 0.0008 0.0001
460,000,000 0.2072 0.3261 0.2567 0.1347 0.0530 0.0167 0.0044 0.0010 0.0002
480,000,000 0.1935 0.3178 0.2610 0.1429 0.0587 0.0193 0.0053 0.0012 0.0003
500,000,000 0.1807 0.3091 0.2645 0.1509 0.0645 0.0221 0.0063 0.0015 0.0003
520,000,000 0.1687 0.3002 0.2671 0.1585 0.0705 0.0251 0.0074 0.0019 0.0004
540,000,000 0.1575 0.2912 0.2690 0.1657 0.0766 0.0283 0.0087 0.0023 0.0005
560,000,000 0.1471 0.2820 0.2702 0.1726 0.0827 0.0317 0.0101 0.0028 0.0007
580,000,000 0.1374 0.2727 0.2707 0.1791 0.0889 0.0353 0.0117 0.0033 0.0008
600,000,000 0.1283 0.2634 0.2705 0.1851 0.0950 0.0390 0.0134 0.0039 0.0010
[/SIZE]
Any entry in the table can be calculated using the following equation:

Prob. = COMBIN(N,K) x (Pwin^K) x (Pnotwin^(N-K))

Where:
N = Number of tickets in play
K = Number of tickets holding the Jackpot combination
Pwin = Probability that a random ticket will win ( = 1 / 292,201,338 = 0.00000000342)
Pnotwin = (1.0 - Pwin) = 0.99999999658
COMBIN(N,K) = number of ways to select K items from a group of N items
x = multiply terms
^ = raise to power (e.g. 2^3 = 8 )

[SIZE=+1]Sample Calculation to Find the Expected Shared Jackpot Amount[/SIZE]
[SIZE=+1] When a Large Number of Tickets are in Play[/SIZE]
​

For this example we will assume the cash value of the Jackpot is $240,000,000 and there are 200,000,000 tickets in play for the current game. Probability values are from the “200,000,000” row above.

[SIZE=-1]Number of Jackpot paid Contribution
winners Probability to each winner (Col 2 x Col 3)
--------------------------------------------------------------
[/SIZE][SIZE=-1]0 .5044 0 0
1 .3452 240,000,000 82,851,815
2 .1181 120,000,000 14,177,179
3 .0270 80,000,000 2,156,379
4 .0046 60,000,000 276,741
5 .0006 48,000,000 30,307
6 .0001 40,000,000 2,881
Other shares 261
Total 99,495,564

[/SIZE]This total then has to be divided by 1 - .5043627 = .495637 to give a weighted Jackpot amount of 99,495,564 / .495637 ~= $200,742,702 which would be used as the payout amount figure used in the “Return on Investment” section below.

These calculations can be used to form an index showing how much the quoted amount of the Jackpot should be reduced to allow for the expected number of co-winners. In the table below, for any given number of tickets in play, the quoted Jackpot should be multiplied by the value in the next column to produce the true expected value of a winning ticket. For example, if there are 200,000,000 tickets in play for a quoted $300,000,000 Jackpot, then the expected value for the Jackpot becomes $300,000,000 x 0.8364 ~= $250,928,378 to adjust for the possibility that a winning ticket will have to split the Jackpot with some other winning ticket.

[SIZE=-1] Number of Mult. Jackpot by Number of Mult. Jackpot by
Tickets this ratio for Tickets this ratio for
in play possible sharing in play possible sharing
0 1.0000 300,000,000 0.7613
20,000,000 0.9830 320,000,000 0.7469
40,000,000 0.9660 340,000,000 0.7327
60,000,000 0.9493 360,000,000 0.7187
80,000,000 0.9327 380,000,000 0.7049
100,000,000 0.9162 400,000,000 0.6913
120,000,000 0.8999 420,000,000 0.6780
140,000,000 0.8838 440,000,000 0.6648
160,000,000 0.8678 460,000,000 0.6519
180,000,000 0.8520 480,000,000 0.6392
200,000,000 0.8364 500,000,000 0.6268
220,000,000 0.8210 520,000,000 0.6145
240,000,000 0.8058 540,000,000 0.6025
260,000,000 0.7908 560,000,000 0.5907
280,000,000 0.7759 580,000,000 0.5791
300,000,000 0.7613 600,000,000 0.5678[/SIZE]

[SIZE=+2]Power Play Option (assume 10x option)[/SIZE]
​

The Powerball game includes an optional “Power Play”. If you spend an extra $1 for the “Power Play”, then the low order prizes are increased as shown in the following table.

The Power Play has a random multiplier as per the following table.

Multiplier times
Multiplier Probability Probability
2X 24/43 1.1163
3X 13/43 0.9070
4X 3/43 0.2791
5X 2/43 0.2326
10X 1/43 0.2326
Sum 2.7674

Thus the expected average total payout if you pay for the Power Play option is 2.7674 times the original payouts. Since you would get the original payouts without paying for the Power Play option, the net value of the Power Play is the increase in payout amounts. This increase in payout amounts is: 2.7674 – 1.0 = 1.7674 times the original payout amounts. We can use this 1.7674 multiplier to calculate the expected return if you pay the extra $1.00 for the Power Play option.
[SIZE=-1]
Payout Increased Exp. Val
Without Payout With Probability Expected After
Match Power Play Power Play of result Value Taxes
5 for 5 not PB 1,000,000 = 1,000,000 8.55574E-08 0.0856 0.0513
4 for 5 with PB 50,000 x 1.7674 = 88,372.09 1.09514E-06 0.0968 0.0581
4 for 5 not PB 100 x 1.7674 = 176.74 2.73784E-05 0.0048 0.0048
3 for 5 with PB 100 x 1.7674 = 176.74 6.89935E-05 0.0122 0.0122
3 for 5 not PB 7 x 1.7674 = 12.37 0.001724838 0.0213 0.0213
2 for 5 with PB 7 x 1.7674 = 12.37 0.001425866 0.0176 0.0176
2 for 5 not PB 4 x 1.7674 = 7.07 0.010872229 0.0769 0.0769
1 for 5 with PB 4 x 1.7674 = 7.07 0.026093351 0.1845 0.1845

Total 0.4997 0.4268
[/SIZE]
Each row shows the combination involved, the payout amount without including the Power Play, the increased payout amount with Power Play included, the probability of the particular output, the expected value for this contribution, and the expected value after 40% is deducted for federal, state, and local taxes. The “Expected Value” is the increase in payout amount times the probability. The total line shows that for each $1.00 that you spend for a Power Play option, you can expect to get back only $0.4997. Taxes reduce this long term expected payout to less than $0.43 for each dollar you pay for the Power Play.

An analysis for Power Play without the 10X option shows the same approximate $0.50 per $1.00 spent return.

[SIZE=+2]Return on Investment[/SIZE]
​

It is interesting to calculate what the long term expected return is for each $2.00 lottery ticket that you buy.

The first task is to construct a table where each row lists the winning combination, the payout, the probability of this payout, and the contribution to the expected return (Equals payout times probability.) The probabilities are the same ones we derived earlier. A $200,000,000 cash payout (decline the annuity) is assumed for the Jackpot. (Would be your portion of a shared Jackpot.)
[SIZE=-1]
Combination Payout Probability Contribution
---------------------------------------------------------
5 White + PB $200,000,000 3.42230E-09 $0.6845
5 White No PB 1,000,000 8.55574E-08 0.0856
4 White + PB 50,000 1.09514E-06 0.0548
4 White No PB 100 2.73784E-05 0.0027
3 White + PB 100 6.89935E-05 0.0069
3 White No PB 7 0.001724838 0.0121
2 White + PB 7 0.001425866 0.0100
1 White + PB 4 0.010872229 0.0435
PB 4 0.026093351 0.1044

Total 0.040213840 1.0043

Total for last 6 rows 0.1796
(Used for after tax calculation)

[/SIZE]
Thus, for each $2.00 that you spend for Powerball tickets, you can expect to get back about $1.0043. Of course you get to pay taxes on any large payout, so your net return is even less.

[SIZE=+1]Expected after tax return on your $2.00 ticket investment when a huge Jackpot is in play[/SIZE]
​

While the above calculation represents an average Powerball game, we might ask what the expected after tax return on your investment might be if a huge Jackpot exists. The following analysis assumes the annuity value of the Jackpot is $2 Billion (that’s a “B”) and there are 600 million tickets in play. The cash value for any Jackpot is about one-half the annuity value which brings the real value down to $1,000,000,000. All prizes of $50,000 and above are reduced 40% to allow for federal and state taxes. Don’t forget that a large prize will throw you into a top tax bracket.

First, let’s calculate the effective Jackpot payout based on 600 million tickets in play. We multiply the “$1,000,000,000 by the 0.5678 value from the 600,000,000 row in the above “Shared Jackpot” table to get $567,800,000 as the shared, before tax effective value of the Jackpot. However, this has to be reduced by 40% for taxes. This leaves an expected after tax value of ~$340,680,000. Finally, we multiply by the probability of winning (1 / 292,201,338) to get an expected after tax contribution from the Jackpot of $1.1658.

Next we include the after tax expected value from the two >= $50,000 prizes. This equals 0.0856+ 0.0548 = 0.1403 less 40% for taxes to give us an additional $0.0842.

Finally, we add in the expected value for the “Total for last 6 rows” This adds another 0.1796 for our expected return. The sum of these three numbers is the expected after tax return for this particular combination. $1.1658 + $0.0842 + $ 0.1796 = $1.4296 expected after tax return for each $2 that you spend per ticket.

[SIZE=+1]Percentile Expected Returns on Ticket Purchases[/SIZE]
​

The average return per $ 2.00 ticket includes the extremely low probability that you might win a large prize – for example $50,000 or more. As a practical matter, it is unlikely that you will ever buy enough tickets (fork out enough money) to ever have much of a chance for any of the large prizes. Thus it is probable that all you will ever get back from your ticket purchases are piddling small amounts.

The percentages for these small amounts can be calculated. The table below shows the percentage chances for various “piddling returns”.

If you spend $2,000 to buy 1,000 tickets (1 ticket for each of 1,000 Powerball games), there is a:
49.67 % chance that you will get back $172 or less
59.94 % chance that you will get back $180 or less
69.98 % chance that you will get back $189 or less
79.76 % chance that you will get back $201 or less
90.08 % chance that you will get back $231 or less
94.97 % chance that you will get back $268 or less
97.98 % chance that you will get back $295 or less
99.00 % chance that you will get back $314 or less
99.50 % chance that you will get back $346 or less
99.88 % chance that you will get back $504 or less

Even if you buy 1,000 tickets, your chance of winning a $50,000 or larger prize is less than 0.12 %.

[SIZE=+1]2nd Thoughts[/SIZE]
​

Government statistics show there are about 1.7 automobile caused fatalities for every 100,000,000 vehicle-miles. If you drive one mile to the store to buy your lottery ticket and then return home, you have driven two miles. Thus the probability that you will join this statistical group is 2 x 1.7 / 100,000,000 = 0.000000034. This can also be stated as “One in 29,411,765-”. Thus, if you drive to the store to buy your Powerball ticket, your chance of being killed (or killing someone else) is about 10 times greater than the chance that you will win the Powerball Jackpot.

Alternately, if you “played” Russian Roulette 100 times per day every day for 79 years with Powerball Jackpot odds, you would have better than a 99% chance of surviving.

[SIZE=+1]3rd Thoughts[/SIZE]
​

A lottery is a “Zero-sum game”. What one group of participants gains in cash, the other group of participants must lose. If we made a list of all the participants in a lottery, it might include:

1) Federal Government (Lottery winnings are taxable)
2) State Governments (Again lottery winnings are taxable)
3) State Governments (Direct share of lottery ticket sales)
4) Merchants that sell tickets (Paid by the lottery organizers)
5) Lottery companies (Hint: They are not doing all this for free)
6) Advertisers and promoters (Paid by the lottery companies)
7) Lottery ticket buyers (Buy lottery tickets and receive payouts)

The winners in the above list are:
1) Federal Government
2) State Government (Taxes)
3) State Government (Direct share)
4) Merchants that sell tickets
5) Lottery companies
6) Advertisers and promoters

And the losers are:
(Mathematically challenged and proud of it)

 

[festeringZit]

BTW, If anyone is curious how they get the 1/~292 million for the odds in hitting the Powerball:

There are 5 main balls from 1-69 and one powerball from 1-26.

So, to hit the main numbers, the formula is a combination of n choose r, which is nCr = n!/ (r!(n-r)!) = 69! / 5! * 64! = 69*68*67*66*65/120 = 11,238,513

Multiply that number by 26 different powerball numbers, and you get 292,201,338

 

[JustinCruise]

good stuff Zit

 

[festeringZit]

What's sick is, say you bought a million dollars worth of tickets (500,000 tickets). Your odds would still only be .0017 chance of hitting.

500,000/292,201,338 = .00171114

 

[JustinCruise]

What's sick is, say you bought a million dollars worth of tickets (500,000 tickets). Your odds would still only be .0017 chance of hitting.

500,000/292,201,338 = .00171114

that's insane

 

[RoofTop]

What's sick is, say you bought a million dollars worth of tickets (500,000 tickets). Your odds would still only be .0017 chance of hitting.

500,000/292,201,338 = .00171114

 

[Vlad the Impaler]

Whoever hits that will have to go into Steve Bartman like hiding. Would be a good problem to have.

You would definitely have to change your phone number. Imagine the organizations and scams that will call you left and right.

For fun, go to ebay and there will be people on there selling "winning lottery numbers"... And this is why I never trust a thing on ebay, they all have great feedback. "I will show you how to hit the lotto every week"

 

[slapshot]

I would think about buying the Colts and trade Luck then get Wilson if possible

 

[JustinCruise]

I would think about buying the Colts and trade Luck then get Wilson if possible

It would be easy


Seahawks would suck your dick for a chance to trade Wilson for Luck.

 

[Vlad the Impaler]

I've said my piece. Just wait is what I will try to leave it out. Does Wilson even have a contract for next season? I guarantee that team knows the real truth. They want to keep him but they know they can't give him what the top level qb's make and be competitive. And his camp probably knows someone will overpay like crazy.

 

[REDEYE]

the way its going Wilson will be underpaid going forward

 

[Vlad the Impaler]

the way its going Wilson will be underpaid going forward

I can't help it, but doesn't that tell you something? Brady, Manning, Rodgers, Brees, Luck, Roethlisberger, Palmer even Eli can basically name their salary yet Russel Wilson can't. Give me all the stupid ass stats you want, but that tells you what the organization truly thinks you are worth. You know why? Because the other qb's I listed can by themselves; basically make you a winner and Wilson can't do it by himself. That is all I have ever been saying.

 

[REDEYE]

if he has great stats he's worthless, if he doesn't have stats he's worthless, doesn't matter what he does, he's worthless to you.. BTW, what has Luck done ?

 

[RenoChazz]

That play in the last game where Wilson managed to avoid a sack and get rid of the ball was impressive.

 

[TomGshotput]

What's sick is, say you bought a million dollars worth of tickets (500,000 tickets). Your odds would still only be .0017 chance of hitting.

500,000/292,201,338 = .00171114

What does Kelly Criterion say about bankroll requirements to buy even one ticket? Calculator I use doesn't work with e-9 probability

 

[Vlad the Impaler]

if he has great stats he's worthless, if he doesn't have stats he's worthless, doesn't matter what he does, he's worthless to you.. BTW, what has Luck done ?

Take a 2-14 team to 11-5 and the playoffs. What happened in the 1 season he missed?

I really don't have anything against you, but can you not see my point? Wilson has had the best defense in the NFL, one of the top 5 running backs in the NFL.. so a running game and a defense...Basically the more talent you have; the more of a cushion you will have. Look at Alex Smith; sucked in San Fran because he was actually counted on. Now in KC is considered above average by most. Same with Matt Cassell, but once you truly give those guys the keys to the car, it wrecks. Wilson will wreck. But I think he has the maturity to not go nuts over it; and will resurface.

 

[REDEYE]

first off that wasn't a 2-14 team... the team had enormous amount of injuries .. so they all came back and the team went 11-5 in a bad division.... big friggin deal... a lot of QB's could have done that.... Wilson overcame a bad O line ,, pedestrian WR''s , and a banged up RB corps

 

[CHOPTALK]

I can't help it, but doesn't that tell you something? Brady, Manning, Rodgers, Brees, Luck, Roethlisberger, Palmer even Eli can basically name their salary yet Russel Wilson can't. Give me all the stupid ass stats you want, but that tells you what the organization truly thinks you are worth. You know why? Because the other qb's I listed can by themselves; basically make you a winner and Wilson can't do it by himself. That is all I have ever been saying.

What are you talking about man?
He just signed a 5 year deal 3 months ago that pays him more then brees

 

[TomGshotput]

If the billboards and newscasters ever announce a $1.7 billion Powerball, the math’s likely to be in your favor.

Now, that’s figure is with a very conservative 200 million tickets sold. If the jackpot actually gets this big, far more tickets could be sold, making the likelihood of a split higher and driving the value of a ticket down—so you’d have to again wait for an increase in jackpot size raise the expected value of a ticket. But then, of course, more people would play, and the single-winner probability would drop again. It’s a vicious cycle.

All that math, just to admit that they got it completely wrong?????

(last drawing they sold over 400 million tickets, pretty obvious an estimate of 200 million for an even larger jackpot isn't going to be right)